Dylan Skinner Porfolio

"Knit your hearts with an unslipping knot."

- William Shakespeare

This project is the backbone of my honors thesis.

My thesis title is: Using Deep Learning Techniques to Find the 4D Slice Genus of a Knot, with abstract:

Deep reinforcement learning (DRL) has proven to be exceptionally effective in addressing challenges related to pattern recognition and problem-solving, particularly in domains where human intuition faces limitations. Within the field of knot theory, a significant obstacle lies in the construction of minimal-genus slice surfaces for knots of varying complexity. This thesis presents a new approach harnessing the capabilities of DRL to address this challenging problem. By employing braid representations of knots, our methodology involves training reinforcement learning agents to generate minimal-genus slice surfaces. The agents achieve this by identifying optimal sequences of braid transformations with respect to a defined objective function.

Ultimately, we used PPO to try and find the minimal slice genus of a knot. You can find all my code here, including my implementation of PPO! (And if you are interested in reading my thesis, you can find it here!)

To see the code used in this project, visit my Github.

Technologies & Tools Used

• Python – Primary programming language for model development.
• Gym (Custom Environment) – Created a reinforcement learning environment tailored to the problem.
• PyTorch – Built and trained custom PPO deep learning models.
• TensorBoard – Visualized training progress and model performance.
• Supercomputer at BYU – Leveraged high-performance computing for multi-GPU large-scale training.

Project Structure

Custom Gym Environment (gym and gym-knot)

To train the agents effectively, I implemented a custom Gym environment, which allowed seamless interaction with the problem space. The repository contains multiple files for environment registration, though only one is necessary—something I’d need to revisit for clarity! If you're interested in custom environments, OpenAI Gym’s documentation is a great resource.

Experimental Results (result_csv)

The result_csv directory holds CSV files documenting various training experiments. Each subfolder represents a separate experiment, labeled as sol_n_m, where:

• n = lower bound for the crossing number used in training
• m = upper bound for the crossing number used in training

Each CSV file records:

• The braid attempted
• Epoch and step when a solution was found
• The reward achieved
• The sequence of moves taken by the agent

Experiments were run in parallel across four GPUs, meaning some experiments may have missing results if certain agents failed to solve their assigned problems.

Training Logs (runs)

This folder contains TensorBoard logs, providing a detailed view of agent performance across different training runs. Due to the sheer volume of experiments, this directory contains a significant number of log files.

Stable Baselines PPO Experiments (tensorboard_stable/updated_logs)

At one point, I experimented with Stable Baselines’ PPO algorithm for comparison with our custom model. Although this approach was ultimately not used in the final thesis, the logs are preserved here for reference.

Model Weights (training_files)

This directory contains saved model weights from various experiments. The most useful files are:

knot_gpu_optim_Large_[number].pt

Here, number refers to the upper bound crossing number. If you want to apply these models to similar problems, use a file where the number is greater than the maximum crossing number you are solving for.

Core Python Files

The repository includes various Python scripts used to develop and train the reinforcement learning model.

• knot_gpu_Large.py – The most important file, containing the model architecture and training loops. This file was responsible for the results presented in my thesis.
• Other Python files – Various iterations of experiments and auxiliary scripts.

Supercomputer Job Script (knot_jobscript)

To efficiently train the model on BYU’s supercomputer, I created a Bash script for job submission. While not required to run the model, this script provides insight into configuring large-scale training runs.

Results

Before addressing the results achieved by our agent, we describe how the agent was trained. Starting off, the agent is given a range of crossing numbers to consider. The environment samples a random knot between those crossing numbers and presents it to the environment. The agent is given 500 chances to solve this knot. (Each epoch provides 100 chances for the agent, so the agent is given 5 epochs total.) If the agent solves the knot 20 times (allowing for the agent to optimize a solution it found for that knot), a new knot is sampled and the agent begins again. If the agent does not solve it 20 times in those 500 attempts, we sample and give the agent a new knot attempt. This process takes approximately 3.5 hours on our GPU for each crossing number range.

We started off by training on knots with five crossings or less, then slowly increased the complexity. We found that allowing our algorithm to see and work on easier knots to solve while still being challenged by higher crossing knots aided in the success of the algorithm long term. In our experiments, our algorithm learned to construct minimal genus slice surfaces for (some, but not all) knots up to 13 crossings.

Training Results

We separate our result figures below into two main parts. The left panel presents the raw training score data. Each graph (and associated color) represents the model's progress on a different GPU. Since we trained on four GPUs at once, we have four different sets of training data. If the agent did not find a slice surface with the correct Euler characteristic for the knot, it was given a reward of -350. Thus, when the agent is successful, the graph contains a spike near 0, but when unsuccessful, the reward does not climb above -350.

The right panel represents the exponential moving average (EMA) for the reward. The exponential moving average places more weight on recent data points, making it more responsive to recent changes. The formula for EMA is given as:

                            EMA_t = (1 - α) * EMA_{t-1} + α * X_t
                        

Where:

• EMA_t is the EMA at time t.
• EMA_t-1 is the EMA at the previous time step.
• X_t is the value of the time series at time t.
• α is the smoothing factor or weight applied to the most recent data point. A smaller α gives more weight to older data.

For these graphs, we used a smoothing factor of α = 0.01. In the initial training stages, the EMA increases, indicating the agent’s improving ability to find surfaces with the correct Euler characteristic. However, as the complexity of knots increases, the agent struggles more. This is expected, as solving more complex knots takes longer.

Training Graphs

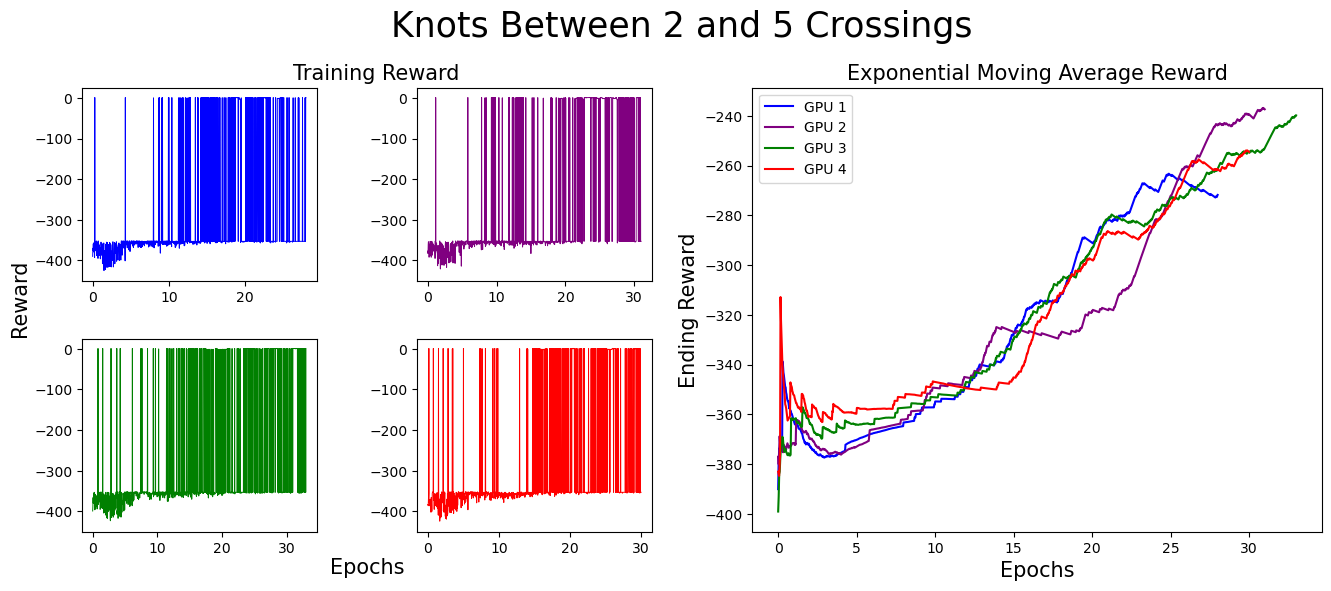
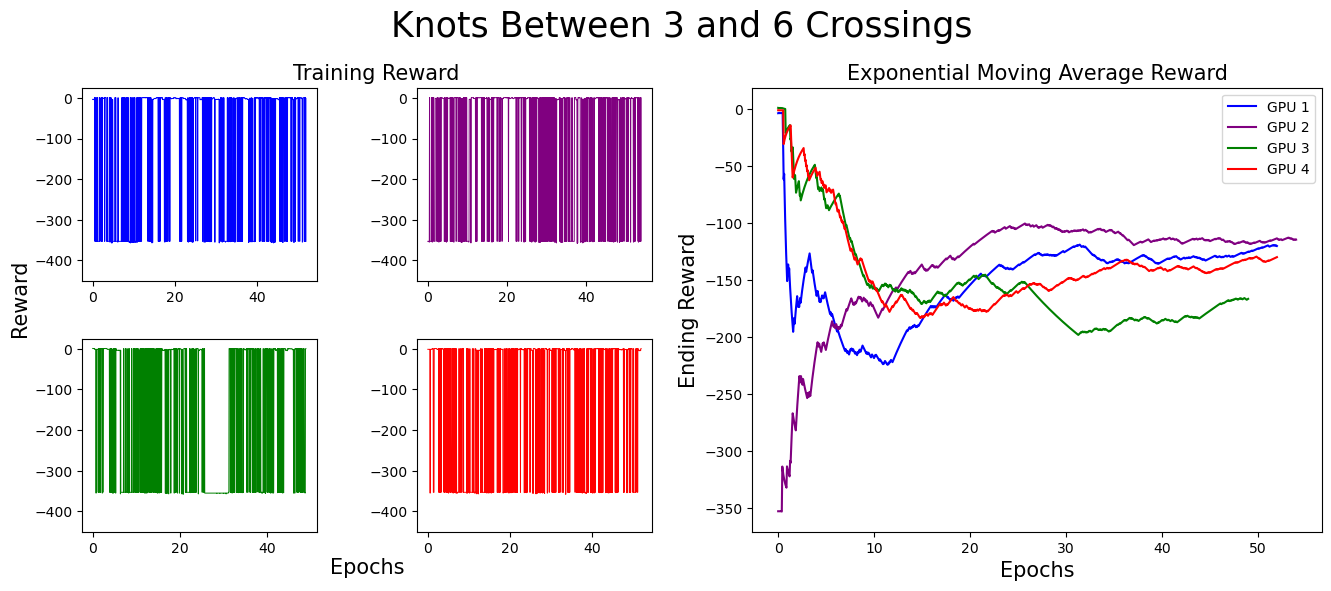
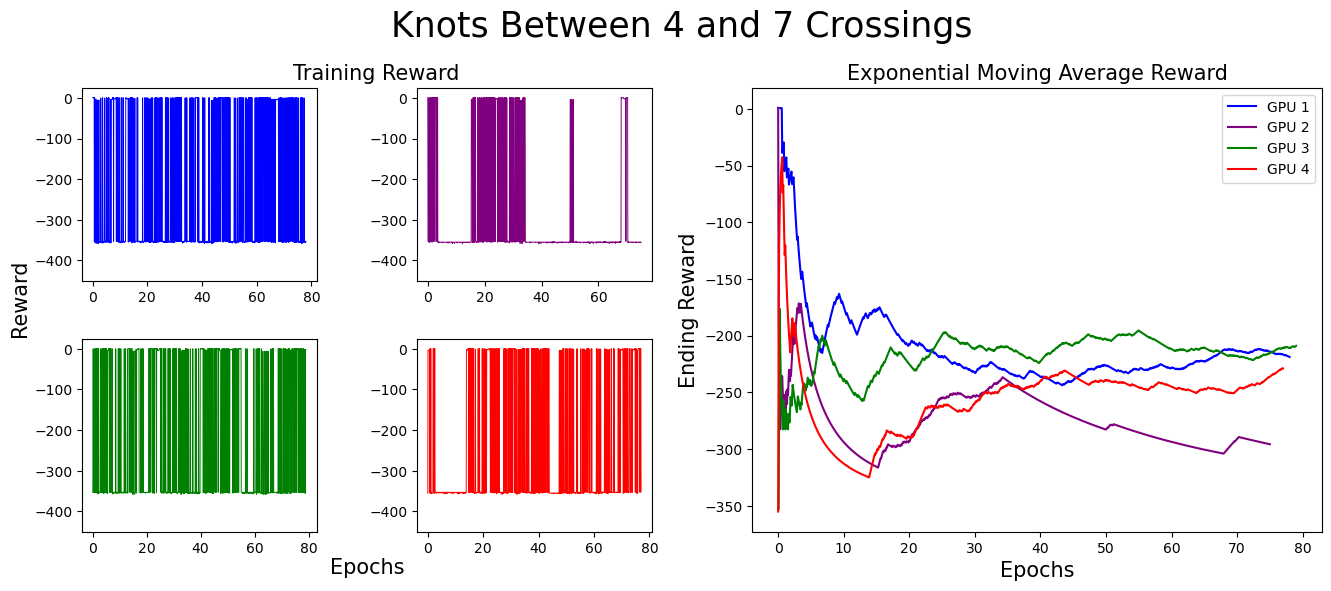
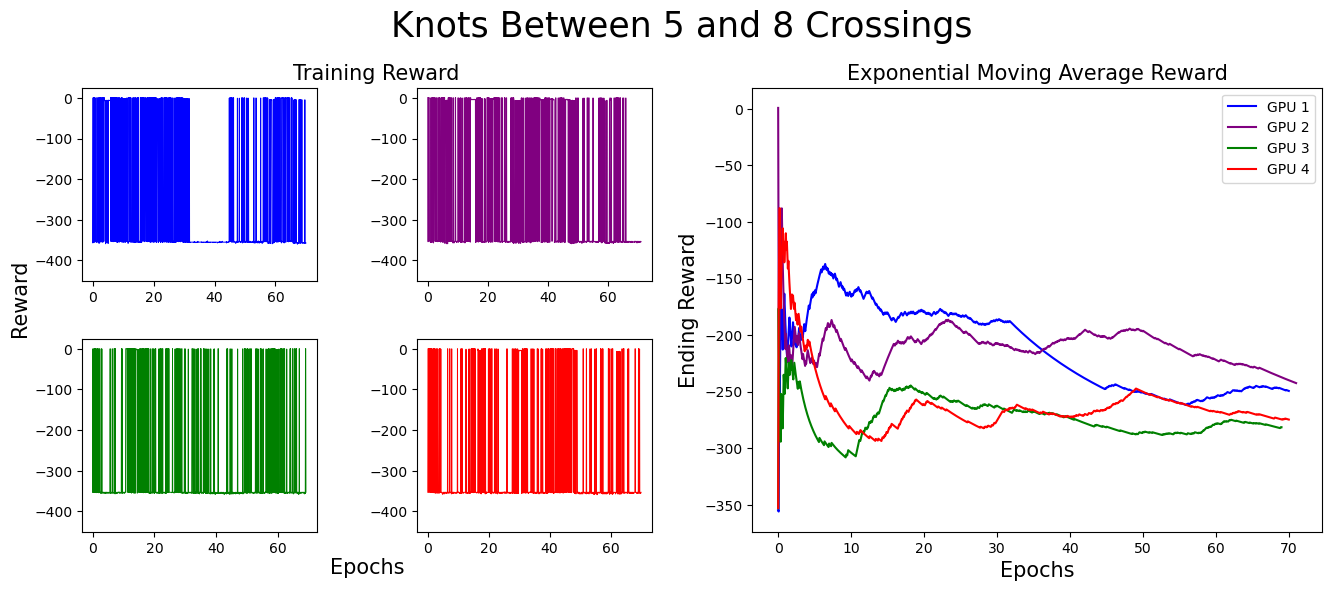
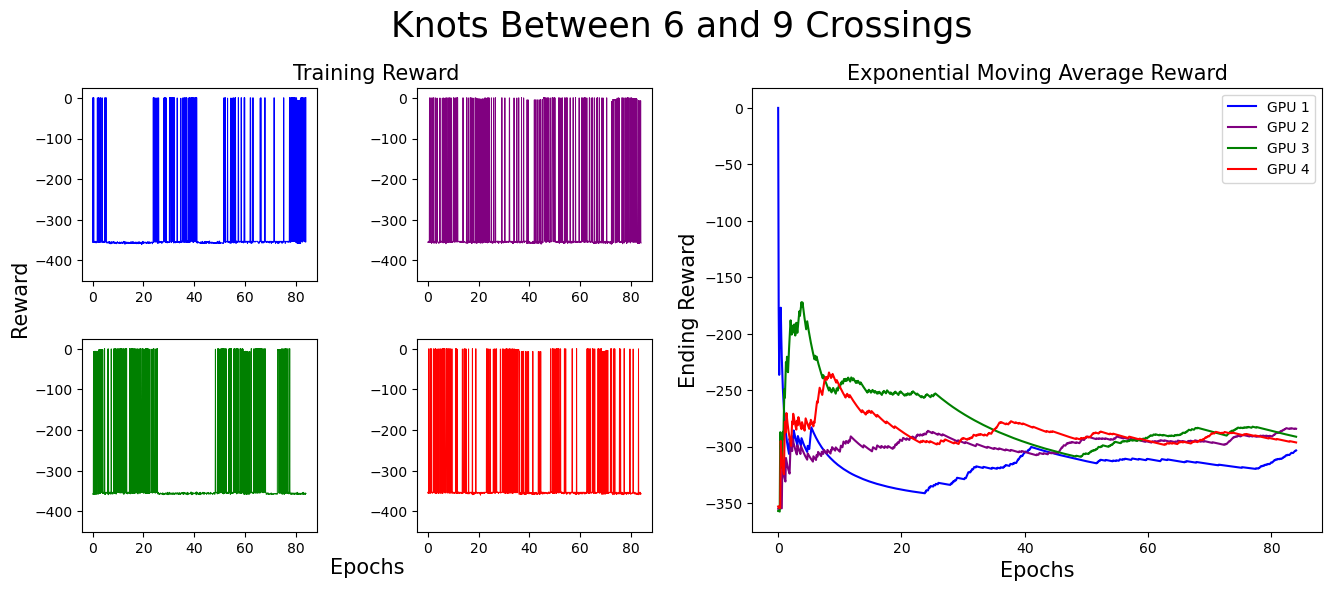
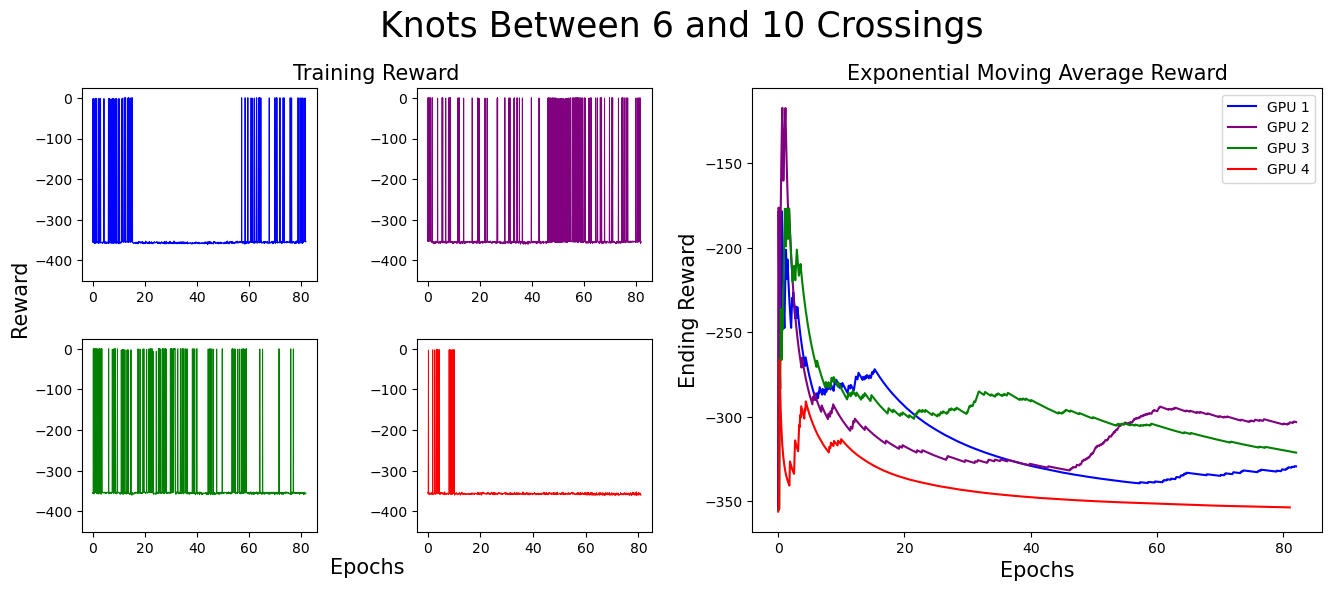
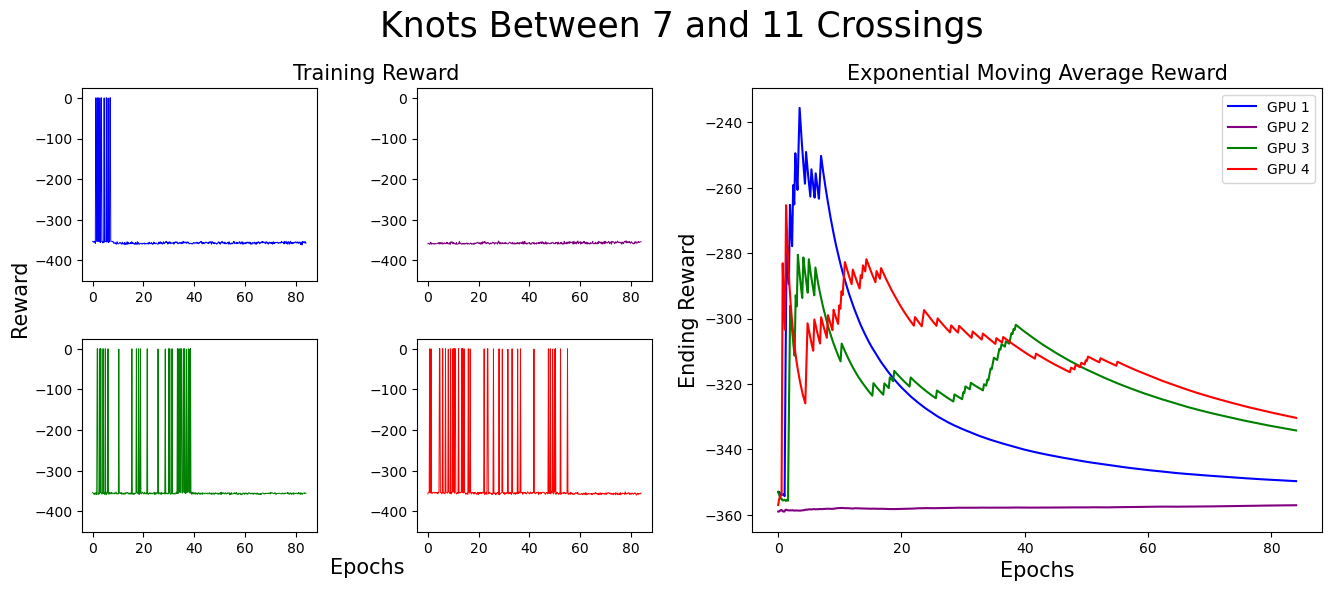
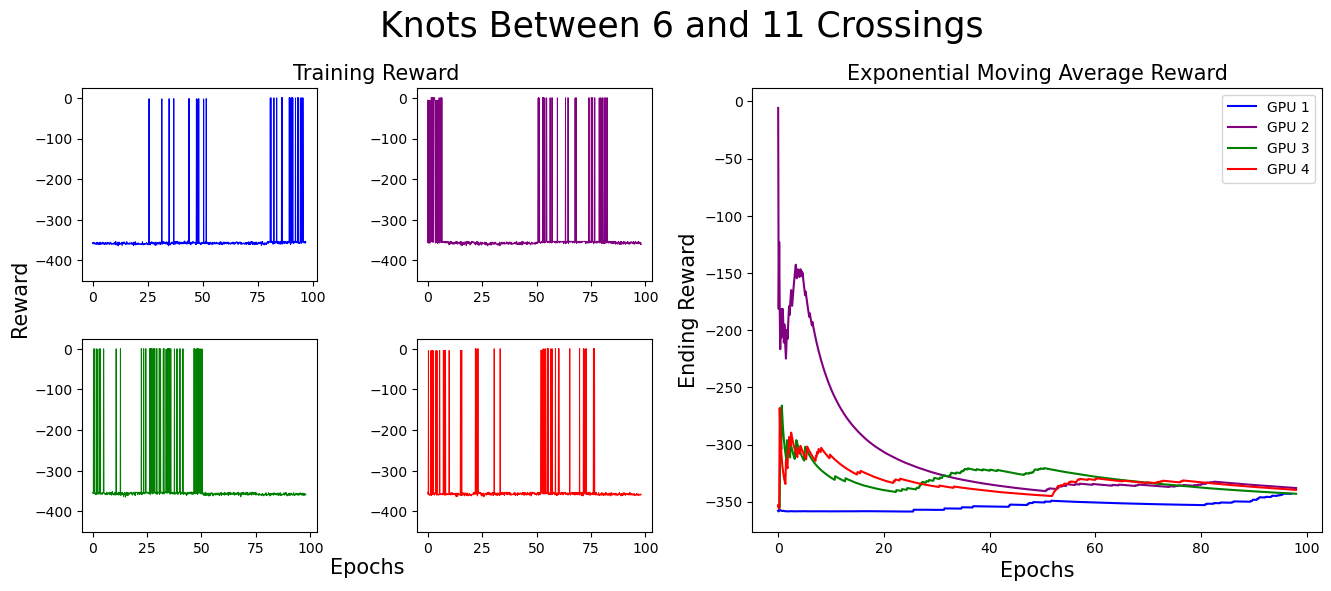
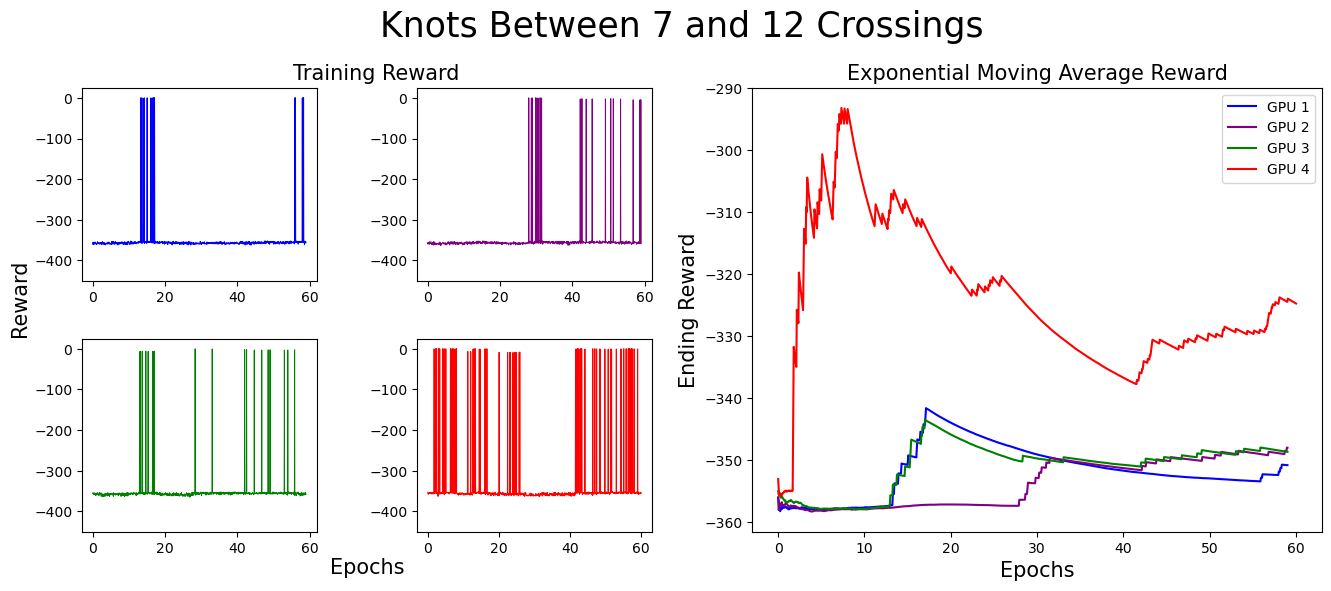
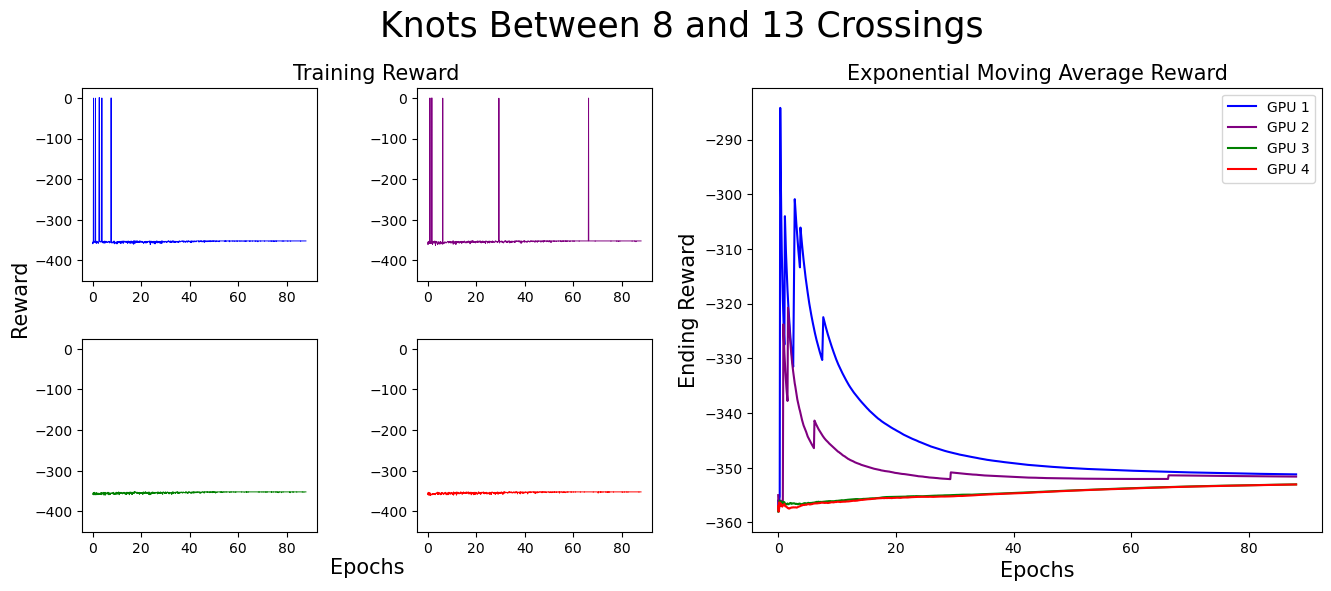
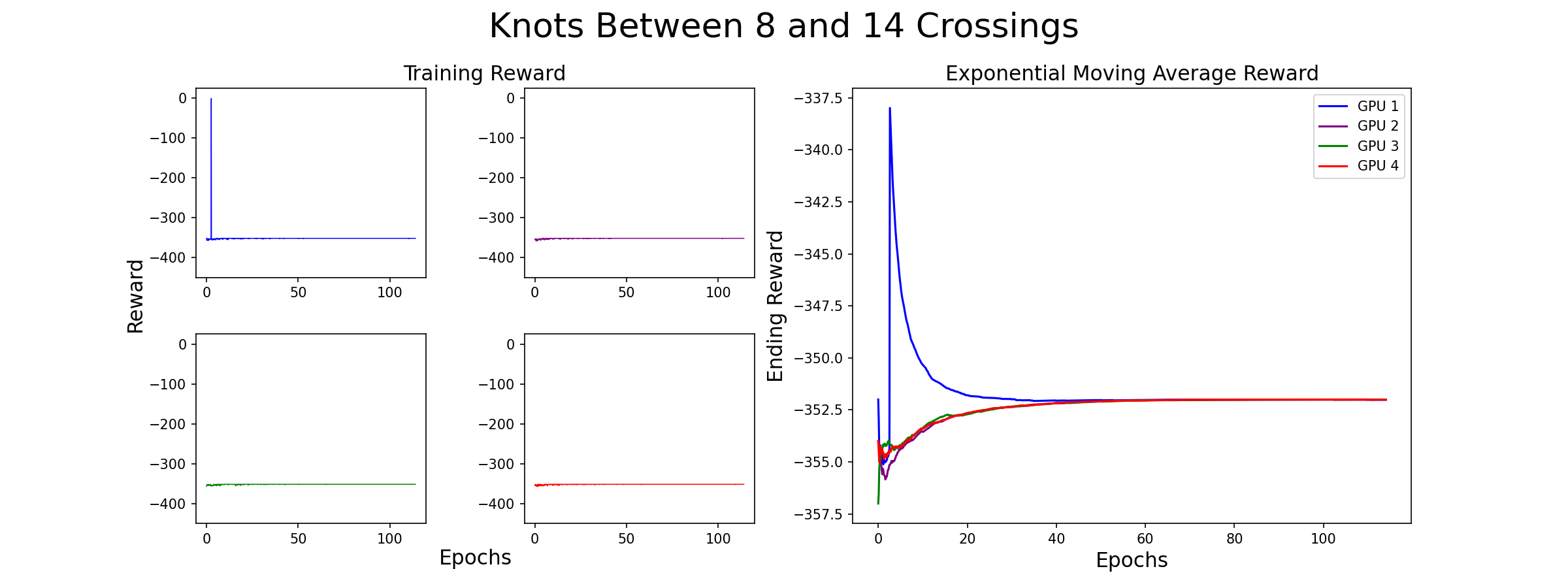
As you can see, the model eventually died...

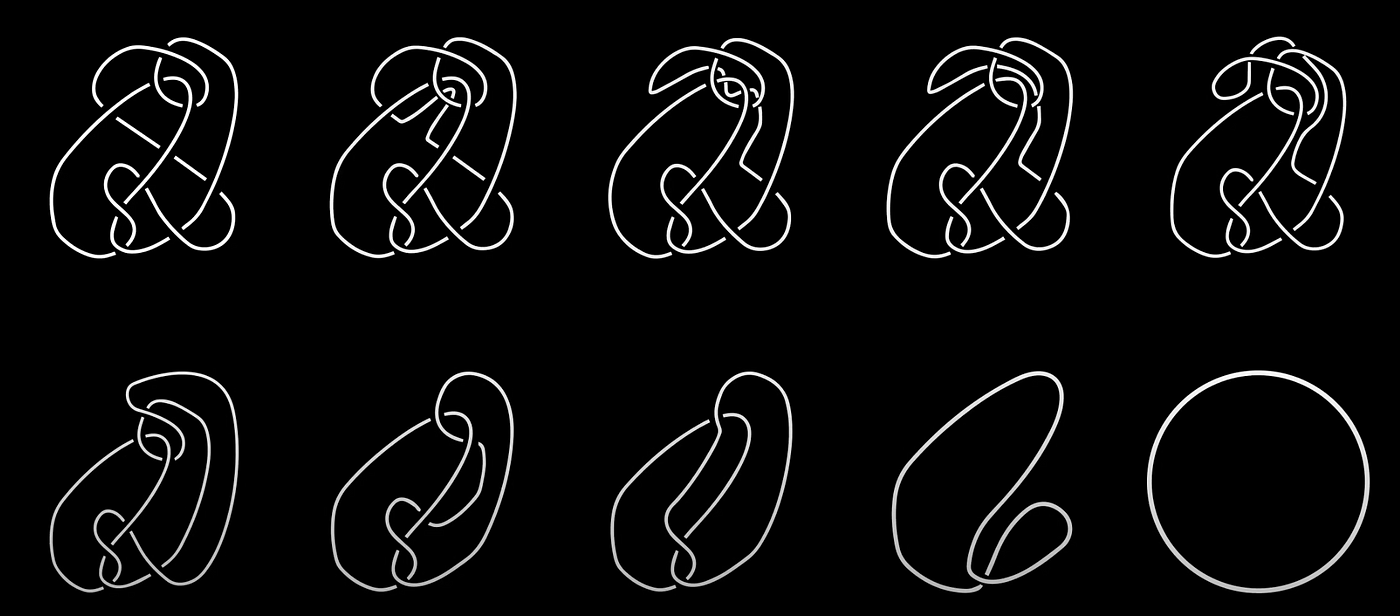
Example of a Successful Solution

Below is an example of our agent finding a minimal genus slice surface for the 10-crossing knot with braid word:

[2, -1, -1, 3, 1, 2, -4, 3, 4, 1]

For this knot, our algorithm received a reward of 0.7 by performing the moves:

[8, 10, 10, 8, 10, 8, 8, 8, 0, 8, 0, 8, 8, 8, 9, 8, 8, 10, 0, 8, 8, 8, 9, 1, 8, 9, 8, 8, 8, 0]

Here is a visualization of these moves being applied to the prescribed knot:

Future Work

One improvement that could be made to this project in the future to improve performance is using GPUs with larger memory capacity. Our model size was ultimately limited to the memory on the GPU, which could very well be what kept us from consistently finding minimal genus slice surfaces for knots with more than 13 crossings.

Additionally, we might not have been using the most effective way to represent knots. The use of alternative knot representation methods (other than braids) could yield more effective approaches, potentially enhancing the overall performance of our deep reinforcement learning model in uncovering the minimal slice genus of knots.

With ongoing research in the Deep RL space new algorithms are being developed which outperform PPO. Exploring and incorporating these future developments will be instrumental in increasing the progress we have made for finding the minimal slice genus of knots.