Dylan Skinner Porfolio

"It's unbelievable how much you don't know about the game you've been playing all your life"

- Mickey Mantle

This project was a joint effort by me and my friend Jason Vasquez. When I say "we," I am talking about me and Jason.

Pitch prediction is a very complicated process that remains (for the most part) unsolved. Many different independent researchers, as well as well-funded MLB analytics departments, have set out to achieve the highest degree of accuracy possible. However, with all of the factors involved, including the unpredictable nature of pitchers, any degree of accuracy that would be noticeably helpful to in-game batters remains elusive. Nevertheless, this problem remains a fun classification/prediction exercise that allows for experimenting with all types of Neural Networks. For our project, we established accuracy baselines, first on random sampling of pitching distributions and then on a shallow CatBoost machine learning model. Then, we iteratively experimented with different models, feature engineering, activation functions, and optimizers to attempt to achieve the highest degree of accuracy we could. Our ultimate goal was to beat 51% accuracy, which was what the author of the dataset on Kaggle achieved by using built-in Keras models.

The Dataset

The data from our dataset was downloaded from Kaggle, courtesy of Paul Schale, it included all pitches from the 2015-2019 MLB seasons including the game situation at the pitch. This data has been widely used for a variety of baseball analytics (sabermetrics) projects.

Dataset Exploration

The data includes a pitches.csv, which includes each pitch, the pitcher id, batter id, game id, and lots of information about the pitch such as spin rate, velocity, break angle, etc. It also contains a prelabeled column pitch type that we will use as our truth values. There is also a file called atbats.csv, which includes information about the specific at bat, including the score, runners on base, result of the at bat, handedness of the pitcher, and handedness of the batter. Finally, there is a players.csv that includes the player name to link to the id's in the above tables. For this project, we want to only use data that would be available to a batter or team before a pitch is thrown, such as the handedness of pitcher, runners on, and most importantly, prior pitches that have been thrown. 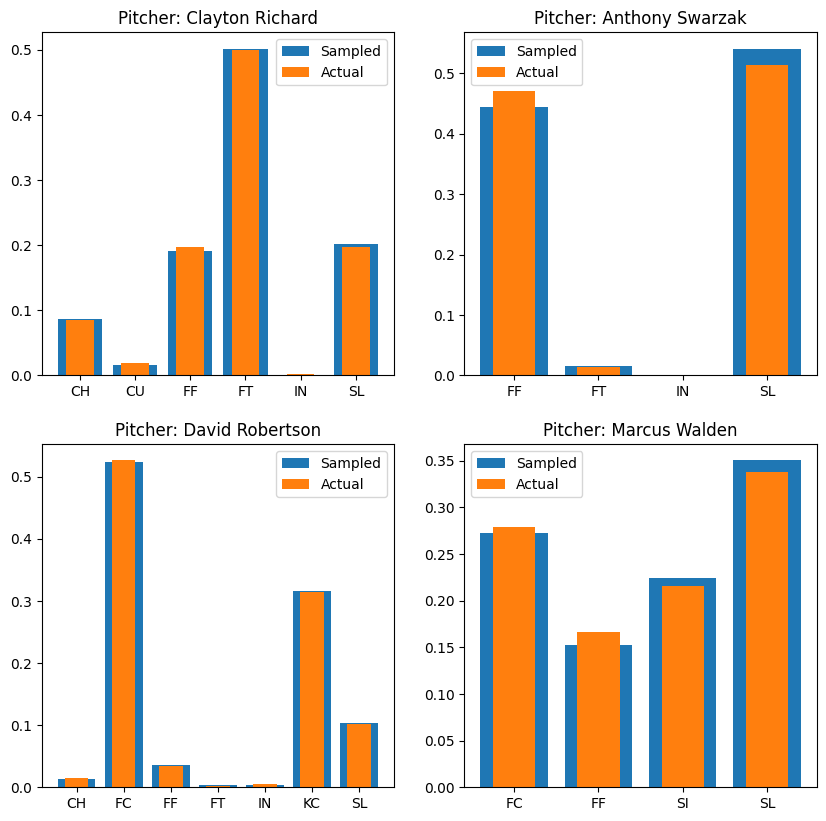We calculated a pitch distribution for each pitcher, and our first accuracy baseline was a model that randomly sampled from the pitcher's distribution for each pitch. Figure 1 below shows the distribution as well as distribution of 2500 random samples for 4 random pitchers in the database. The random model produced an accuracy of 32.9%.

Our Methodology

After our random model, we established another random baseline by fitting our data to a shallow machine learning classifier, CatBoost. This model achieved a 45% accuracy. Our goal was to be higher than 51% with a Deep Learning model.

To prepare the data, we randomly split pitches into training or testing data using the built-in sklearn.model_selection.train_test_split(). With the data split, we prepared the data by combining the data frames and filtering out the columns we wouldn't use for our model. We were left with 15 features, namely pitcher name, pitcher handedness, batter, batter stance, batter score, ball count, strike count, outs, runner on 1st, runner on 2nd, runner on 3rd, inning, pitcher score, and game id. We also had approximately 3.5 million pitches in our dataset, and about 80% of those were in our training data, leaving about 20% for our testing data.

Our first approach was thinking that a Recurrent Neural Network would be the best model for this task. This would allow us to treat a game like a paragraph, with each pitch a character. Because of the nature of baseball, past pitches (and their success rate) influence future pitches, so we were hopeful a type of RNN model would capture the patterns and learn how to predict future pitches from past pitches. This provided some difficulties with the data cleaning, as we had to treat a game of pitches like a sequence, and then pass in one game at a time to our model. However, as the games have different amounts of pitches, we had to pad them which provided some difficulties. We also tried not padding or batching the pitches and passing one pitch at a time to the RNN, reinitializing the hidden layer every game, but this did not provide us with the accuracy we were hoping for. Experimenting with an LSTM gate, and a GRU cell provided marginally better accuracy than vanilla RNN, but we were still topping out in the low 40s.

After this, we thought that a transformer with self-attention would be a good way to capture the sequential patterns in the data. With the data still grouped by game and padded, we passed it through a self-attention transformer. This also slightly bumped up our accuracy, but not to the levels we were hoping for or believed we could get. At this point, we shifted our approach, we stopped grouping the data by games and realized that feature engineering might be able to unlock higher accuracy for us. We went through the data, added a column (feature) for each pitch type, and then filled in the columns with how many pitches of that type the pitcher had thrown up to that point in the game. So at the beginning of the game, all of those columns were 0, but as the pitcher started to throw pitches the columns would populate with past pitch types. This allowed us to batch the data and not group it by game, which provided for much faster and more efficient training, but it still had the sequential information that was needed for accuracy. In a way, it became a pseudo-markov chain because each row of data contained all of the information it needed about past events in its current state. However, as each row only knew about past pitches, this didn't violate the principle of being able to predict pitches in real-time.

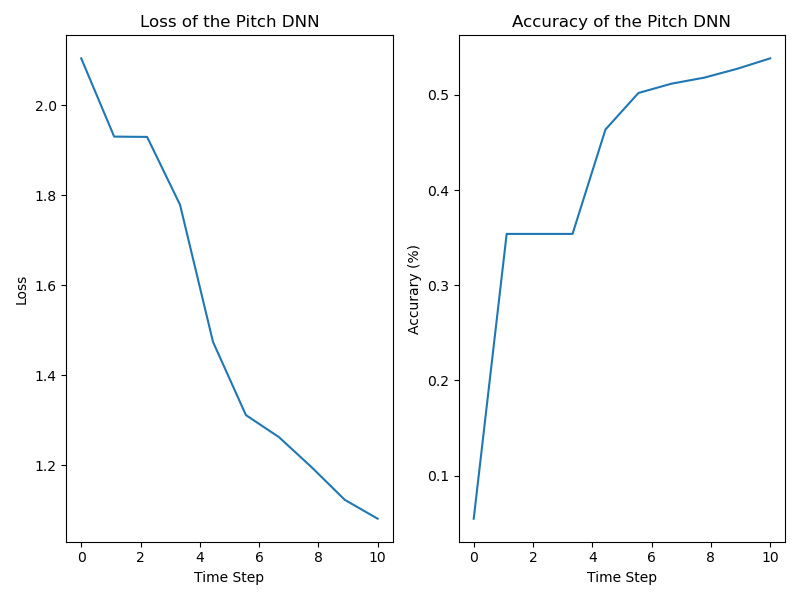
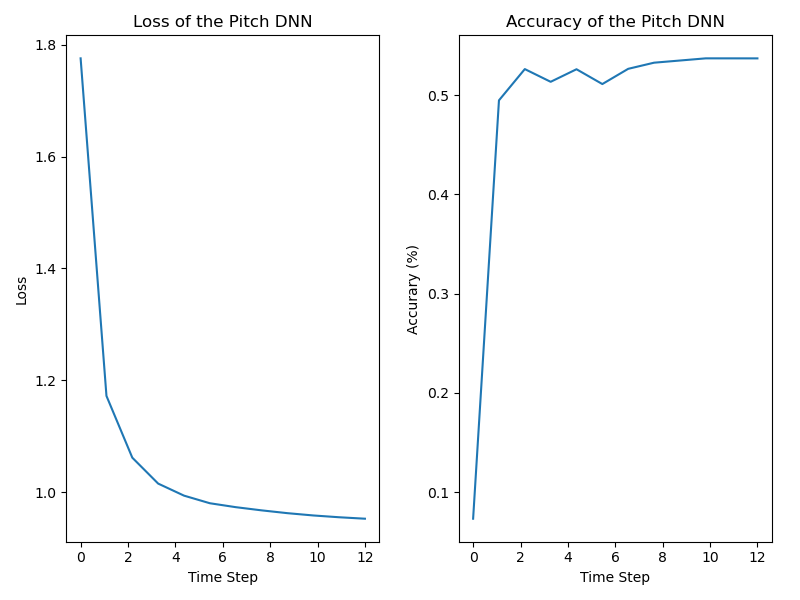
With our updated dataset, we shifted the focus of our model to dense linear networks, and experimented with several different amounts of layers, activation functions, etc. We found that this method worked best of all, and initially saw a result of around 51%. We also formatted the code in a way that allowed us to run it on the supercomputer so we could train for longer with denser networks. With using the AdaBelief optimizer, and Penalized TanH as an activation function on our deep model, we achieved accuracy of around 55% after 10 epochs of training. Then, as a final experiment, we attached a self-attention transformer to our linear model, and found that while the final accuracy didn't improve all that much, the network trained much faster, which is still an improvement. Figure on the top is the test accuracy with the deep linear model, and the figure on the bottom is with the transformer in the model.

Analysis

After experimenting, we were able to achieve 54-55% accuracy on our test data, and the average for the training data accuracy was in the same range. We consider this a success, as it beats our baseline accuracy models, and beats the 51% accuracy that the author of the dataset achieved in his Kaggle post. We consider the most important element to our increased accuracy to be the novel techniques we used on our model and the feature engineering that encoded important information in the dataset before training. Our first approach of using a Recurrent Neural Network was not our final approach, because it did not achieve our accuracy goal, and after several iterations we were able to achieve higher accuracy without an RNN. We believe that one limitation that we had was the scope of our data. We had access to 4 seasons of pitch data which only provided just over 3 million pitches. We are hopeful that with more data and more experimentation, we could achieve even higher results.

To see all of our code, please visit our Github.